The Floyd–Warshall algorithm is an example of dynamic programming, and was published in its currently recognized form by Robert Floyd in 1962. It is also known as all pair shortest path problem. Floyd–Warshall algorithm is an algorithm for finding shortest paths in a weighted graph with positive or negative edge weights (but with no negative cycles).
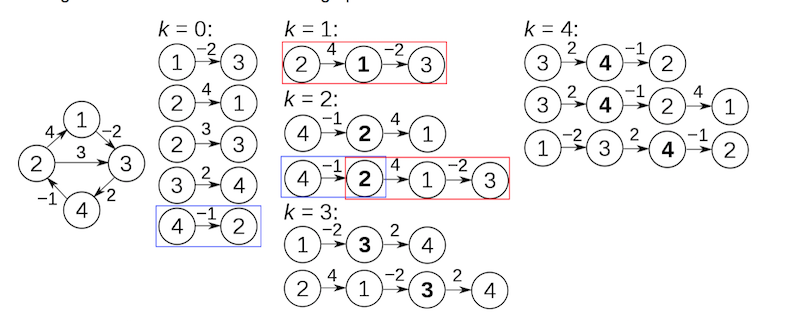
The Floyd–Warshall algorithm is a good choice for computing paths between all pairs of vertices in dense graphs, in which most or all pairs of vertices are connected by edges. For sparse graphs with non-negative edge weights, a better choice is to use Dijkstra’s algorithm from each possible starting vertex, since the running time of repeated Dijkstra using Fibonacci heaps) is better than the running time of the Floyd–Warshall algorithm when “E” is significantly smaller than “V2” For sparse graphs with negative edges but no negative cycles, Johnson’s algorithm can be used, with the same asymptotic running time as the repeated Dijkstra approach.
